Solving problems with Recursion can be challenging, though the logic is always same, break down the given problem into smaller problems.
This article will dive deep into a problem based on recursion. We'll assume that you have an idea about what recursion is.
Feel free to take pauses while we are solving, and try it on your own first. Let's dive in!

Problem statement

You are given an array of unique elements and a sum. You need to calculate the number of subsets of the given array, whose sum is equal to the given sum. Let's understand this with the help of an example.

Input: {10, 5, 2, 3, 6}
sum = 8
Output: 2

The two subsets of {10, 5, 2, 3, 6} with sum 8 are {5, 3} and {2, 6}. So, we return 2.

Input: {1, 2, 3}
sum = 0
Output: 1

There will be only one subset of {1, 2, 3} i.e empty set {} with sum 0. So, we return 1.

Stop. Think about it before going to the approach.

Approach

Before we can check the sum of a subset, we need to first think about reaching to the subsets from the given set.
Let's understand this by taking {1, 2, 3} as the given set.
You need to think of a way by which you can generate subsets of {1, 2, 3} if you have the subsets of {1, 2}. Notice, from the above tree diagram, we can make subsets of {1, 2, 3} from subsets of {1, 2} by deciding whether the next element i.e 3 would be added to the set or not.

Stop. Think again!

Now, to make things even clear, here is another tree diagram for you.

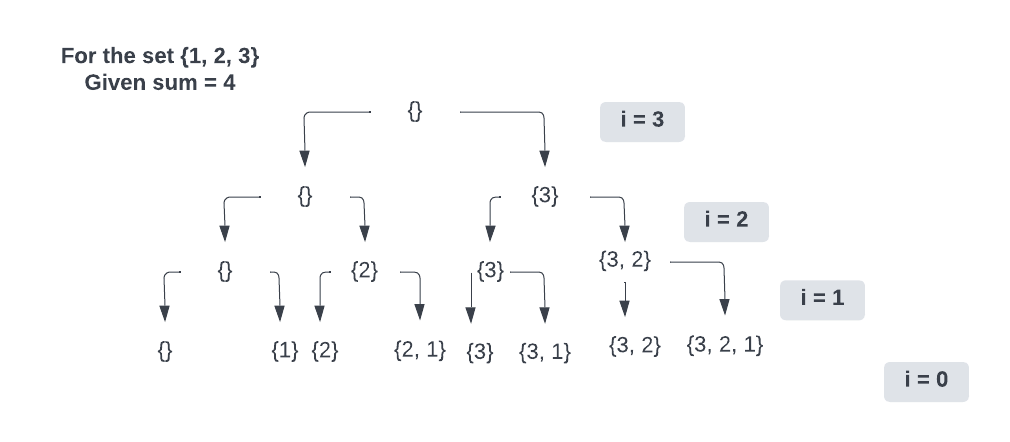
You might have guessed from the above tree, we'll need a variable as a parameter to the function, that we will use to traverse the array, let's name it 'i'. When i becomes 0, we have all the subsets from the given set.

Now that we have the subset, how can we manage the sum variable while recursively calling for the function? Give it a thought and come back.

Coming to the original problem, we need to find the count of subsets with sum equal to the given sum.

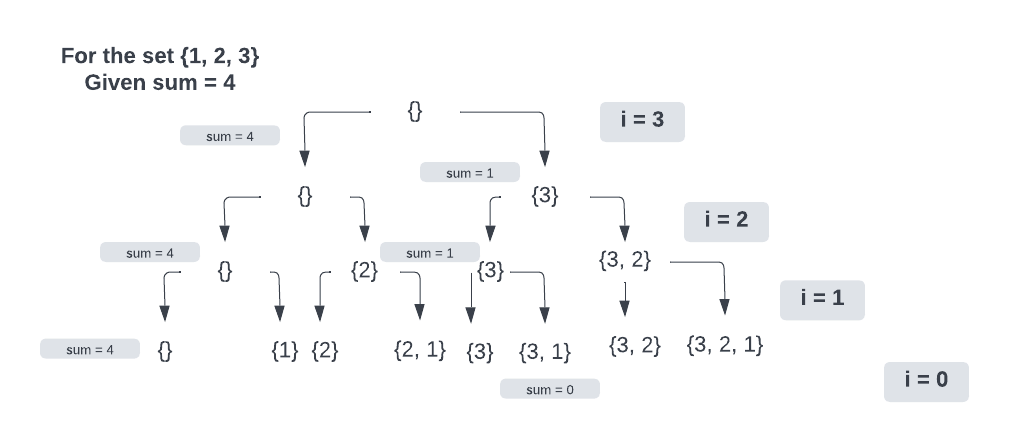In the above tree, whenever we add a new element to the set we reduce the sum by the value of that element. In this way, we will have the sum value as 0 for the required subset.
If the sum value is 0 in the base case i.e (i ==0) we return 1, otherwise, we return 0.

Stop. Before moving to the solution, try to write code on your own in your favorite programming language.

Solution

Here is the full code for this problem in C++

int countSubsets(int arr[], int n, int sum)
{
    if (n == 0)
        return sum == 0 ? 1 : 0;
    return countSubsets(arr, n - 1, sum) + countSubsets(arr, n - 1, sum - arr[n-1]);
}


int main() {
        int n = 3, arr[]= {10, 20, 15}, sum = 25;
        cout<<countSubsets(arr, n, sum);
        return 0;
}

Time Complexity

Since every call of countSubsets is taking only constant time. We just need to find the number of recursive calls to calculate the time complexity. We can find this easily by using the recursion tree that we made above.

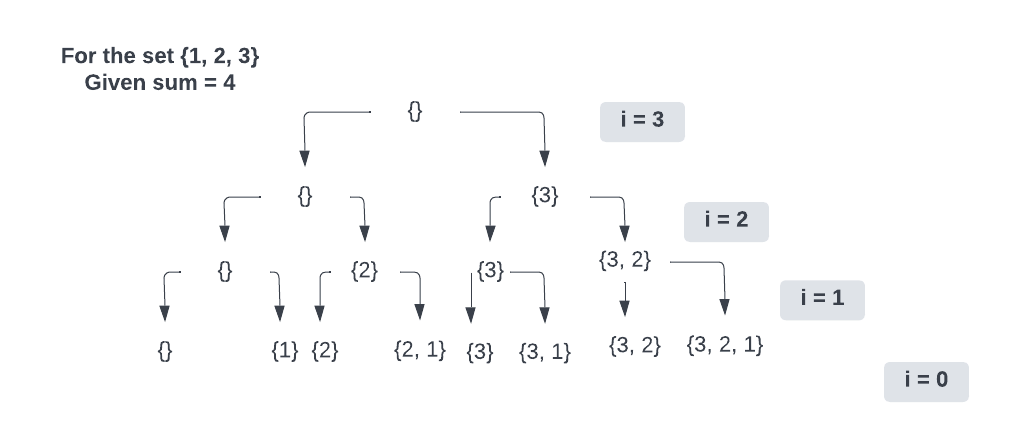
Let countSubsets takes k time before calling itself again.
Total time for the problem will be: k(1 + 2 + 2^2 + 2^3 . . . . . . n times) We know that, this is a geometric progression with common ratio 2. So, total time will be dependent on 2^n.
Hence, Time Complexity for our solution becomes Theta(2^n)

That's it, folks! Hope this made you more clear about recursion. Keep learning, keep hustling!